【Three.js】Tweenでオブジェクトを球状に並べる方法

2021年2月6日JavaScript,Three.js

学生時代のツケ

はじめに

前回はTweenを使ってオブジェクトを整列させてみました。今回はオブジェクトを球状に並べます。three.jsの公式サイトを参考にさせてもらいました。

↓こちらが完成したものです。

デモサイトはこちら。

そして、パネルを球状に配置する処理は↓こんな感じです。

// 集合
function gather() {
  TWEEN.removeAll();
  
  const vector = new THREE.Vector3();
  const len = panels.length;
  
  for (let i = 0; i < len; i++) {

    /***** 移動先となる座標を持つオブジェクトを作る ここから *****/
    const phi = Math.acos(-1 + (2 * i) / len);
    const theta = Math.sqrt(len * Math.PI) * phi;
    const sphericalPos = new THREE.Spherical(500, phi, theta);

    const target = new THREE.Object3D();
    target.position.setFromSpherical(sphericalPos);

    vector.copy(target.position).multiplyScalar(2);
    target.lookAt(vector);
    /***** 移動先となる座標を持つオブジェクトを作る ここまで *****/

    // パネルの位置
    new TWEEN.Tween(panels[i].position)
      .to({x: target.position.x, y: target.position.y, z: target.position.z}, 1000)
      .easing(TWEEN.Easing.Exponential.InOut)
      .start();

    // パネルの向き
    new TWEEN.Tween(panels[i].rotation)
      .to({x: target.rotation.x, y: target.rotation.y, z: target.rotation.z}, 1000)
      .easing(TWEEN.Easing.Exponential.InOut)
      .start();
  }
}

何やってるかをざっくり言うとですね、

移動先の座標を持つ"target"という名前のオブジェクトを作る
Tweenを使って、"target"の座標に向かってパネルを移動させる
Tweenを使って、"target"の傾きに向かってパネルを傾かせる

ざっくり。1で作った"target"は画面には映りません。その位置にあるんだけど見えない、みたいな。見えないけれど確かに存在する星の王子さま的なソレに向かってパネルは動いていくという仕組みです。なるほど…。

わからん

for (let i = 0; i < len; i++) {
  const phi = Math.acos(-1 + (2 * i) / len);
  const theta = Math.sqrt(len * Math.PI) * phi;
  const sphericalPos = new THREE.Spherical(500, phi, theta);
  (略)
}

ここがわからん！急に数学的なヤツを…！

というワケで今回はココを掘り下げていこうと思います。

phi

…ピ、ピヒ、…フィ？あっ、フィ!？フィ……。カタカタカタ、タン。

ファイ

ファイでした。地球の緯度を表現する時によく使われる言葉らしいです。赤道が0度で北極点が北緯90度で南極点が南緯90度。

それが分かると2行目のは何してるかわかりますね。パネルの緯度を決めているんですね。て事は3行目の…

theta

…カタカタ、ッターン！シータはパネルの経度を決めているに違いない。

それが分かったところで本題に行きましょう。まずは2行目のヤツからです。

Math.acos(-1 + (2 * i) / len)

“acos"はアークコサインです。三角関数のヤツ。引数にコサインの値を渡すと角度をラジアンで返してくれます。

普段使ってる"度"に"π/180″を掛けてあげるとラジアンになります(πは円周率のパイです)。逆に"度"をラジアンにしたい時は、ラジアンに"180/π"を掛けてあげましょう。なので、180度をラジアンで表すとπになります。

いまいちピンときませんが、とりあえず「そういうものなんだ」と思うことは意外と大事。

“i"には0～29の値が順番に入り、"len"はパネルの個数である30が入ります。計算していくとこうなります。

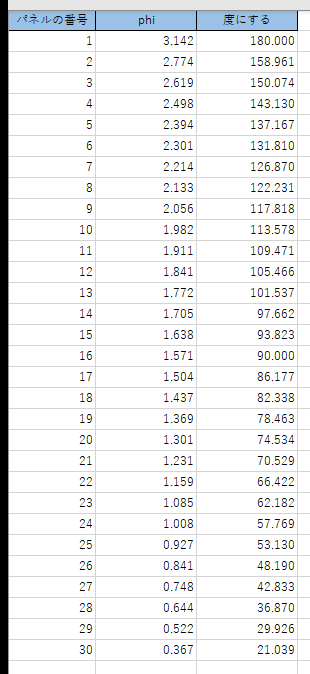
こんな感じ。180度から始まって、どんどん0度に近づいていきます。デモサイト見てもらうと分かりますが、1番のパネルは南極点の位置にあって、30番のパネルは北極点に少し届かない位置にあります。まさにこの計算結果の通りですね。これでパネルの緯度が求められました。次は経度です。

const theta = Math.sqrt(len * Math.PI) * phi

“sqrt"で平方根を求める事ができます。パネルの数に円周率かけたヤツの平方根求めてさっきはじき出した緯度をかけてあげれば経度が出るワケですね。大丈夫です。僕も自分が何言ってんのか分かりません。

これホントに分からないですねぇ。理屈がまったく分からない。「これで経度が出ますよー」っていう数学の公式的なものなのか、それともこのプログラム書いた人が「できたー！この計算式でイイ感じにパネルの位置決められるじゃん！」って独自に編み出したものなのか、それすら分からない。

しょうがないから理屈を知るのは諦めて計算だけしてみましょう。

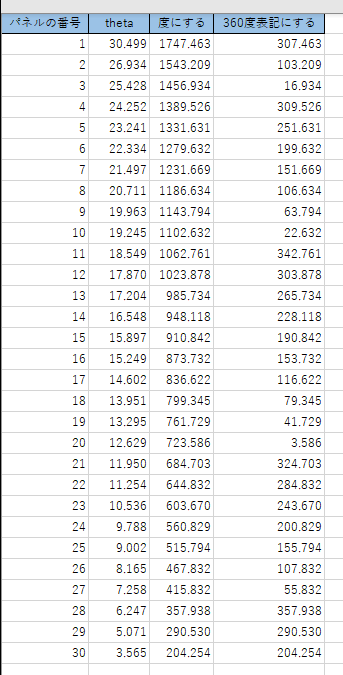
計算結果を見ると「たしかにそうなってますねぇ」と思います。実際に球体を見てみると、1番と4番のパネルはほぼ同じ角度のところにいますもんね。うーん、とりあえずコレでよしとしましょう。

const sphericalPos = new THREE.Spherical(500, phi, theta);

ここまで来るとコレはなんとなく分かりますね。3D空間の原点から半径500の球体を作って、その表面の座標の情報を持つオブジェクトを作っているのでしょう。で、その位置に"target"をセットするという事です↓。

const target = new THREE.Object3D();
target.position.setFromSpherical(sphericalPos);

というワケで

ちょっと釈然としない部分もありますが、よくよく考えたら、パネルの位置なんて自分の好きなように決めちゃっていいんですよね。それが球体に見えるのであれば。

緯度と経度さえこっちで決めてあげれば、あとは"THREE.Spherical"が勝手に球面上の座標を考えてくれるんですから。また時間あるときにでも試してみます。今回は以上です。ありがとうございました。

おしゃれ度

★★★☆☆

Posted by ナカタ