【WebGL】トーラスの座標の求め方

これで分かるかしら…。
はじめに
WebGLを勉強中なんですけど、最近はwebgl.orgをよく見ています。非常に分かりやすいです。ありがとうございます。
で、その中でトーラスモデルの座標の求め方が紹介されていました。コレです↓。
function createTorus(row, column, irad, orad) {
let pos = new Array();
for (let i = 0; i <= row; i++) {
let r = Math.PI * 2 / row * i;
let rr = Math.cos(r);
let ry = Math.sin(r);
for (let j = 0; j <= column; j++) {
let tr = Math.PI * 2 / column * j;
let tx = (rr * irad + orad) * Math.cos(tr);
let ty = ry * irad;
let tz = (rr * irad + orad) * Math.sin(tr);
pos.push(tx, ty, tz);
}
}
return pos;
}ムズくてよく分からんですね…。
でも、これコピペすると確かにできるんですよねぇ。ドーナツみたいな輪っかが。
でもなんでコレで座標が求められるのか分からないからモヤモヤするわけですよ。
そんなワケで色々調べたり考え込んだりして解明しました。
引数の説明
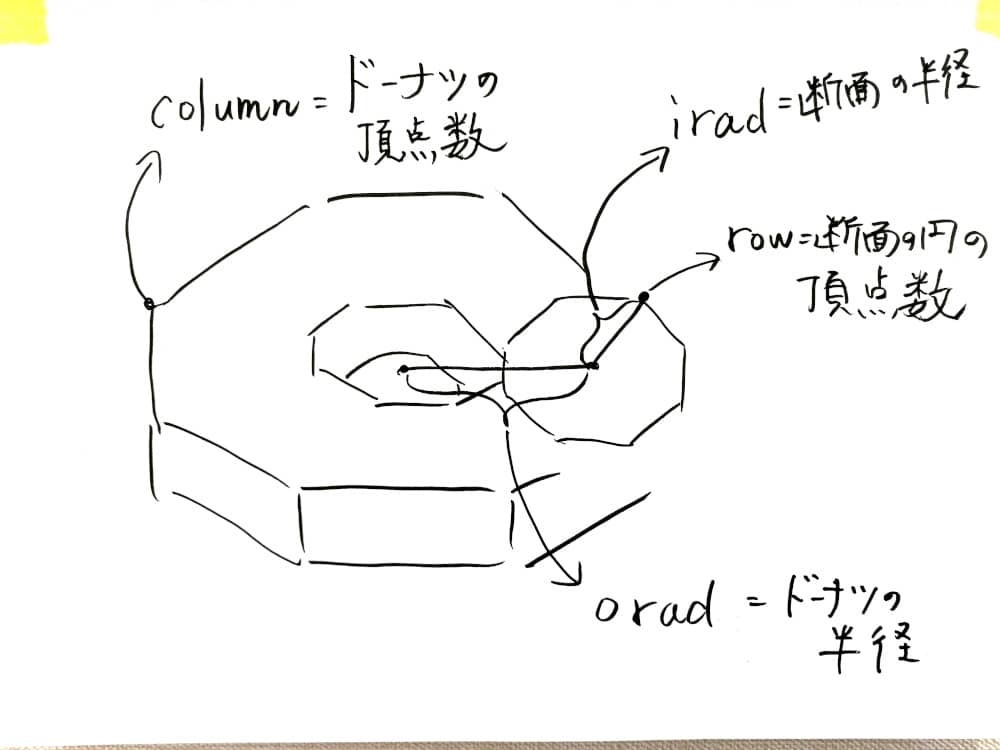
iradでドーナツの太さを、oradでドーナツの大きさを決めているワケですね。
rowとcolumnは頂点数。値が小さいとカクカクになって、大きいと滑らかになります。
上から順に見ていきましょう
まずは先頭でやってるコレ↓。
for (let i = 0; i <= row; i++) {
let r = Math.PI * 2 / row * i;
// ・・・コレは断面の円の各頂点までの角度をラジアンで求めています。絵で書くとこうです↓。
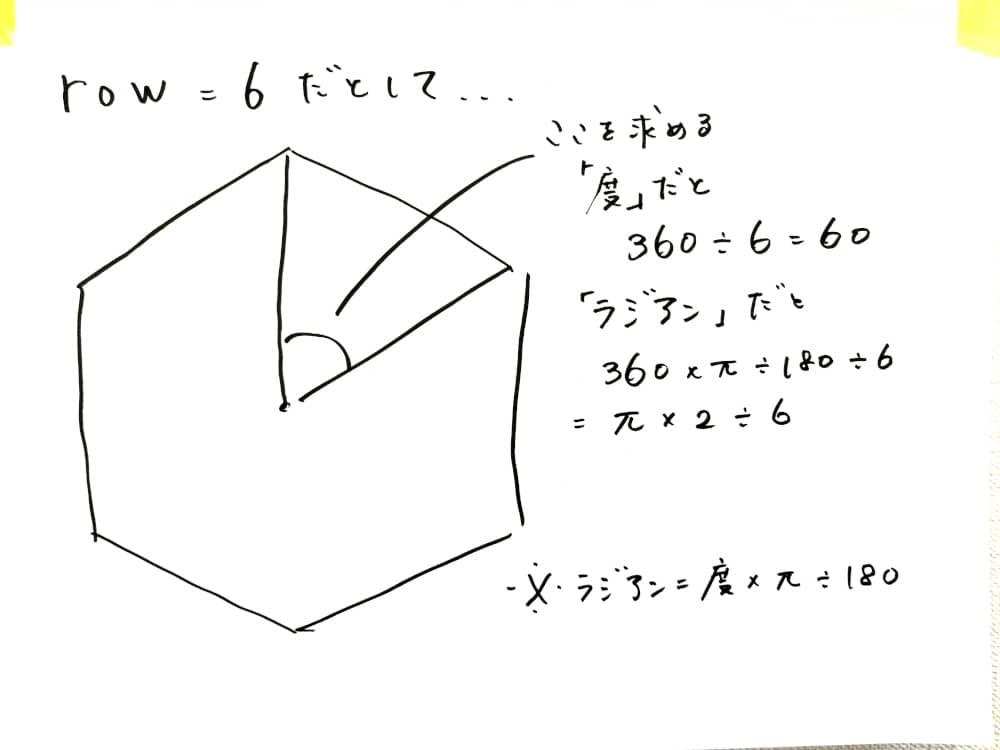
全ての頂点について角度を求めたいのでループに入れてiを掛けています。
角度が分かったので、それを使って頂点のx座標とy座標を求めます。
for (let i = 0; i <= row; i++) {
let r = Math.PI * 2 / row * i; // 断面の円の各頂点までの角度(ラジアン)
let rr = Math.cos(r); // 断面の円のx座標
let ry = Math.sin(r); // 断面の円のy座標
// ・・・ここで求めたx座標とy座標は半径が1の断面の中心を原点としたときの値になりますので、そこだけ注意です。ドーナツの中心が原点ではありません。そこんとこよろしくお願いします。
続いて内側のループです。
for (let i = 0; i <= row; i++) {
let r = Math.PI * 2 / row * i; // 断面の円の各頂点までの角度(ラジアン)
let rr = Math.cos(r); // 断面の円のx座標
let ry = Math.sin(r); // 断面の円のy座標
for (let j = 0; j <= column; j++) {
let tr = Math.PI * 2 / column * j; // ドーナツの各頂点までの角度(ラジアン)
// ・・・内側ループの先頭はさっきと同じですね。各頂点までの角度を求めています。はい次。
for (let i = 0; i <= row; i++) {
let r = Math.PI * 2 / row * i; // 断面の円の各頂点までの角度(ラジアン)
let rr = Math.cos(r); // 断面の円のx座標
let ry = Math.sin(r); // 断面の円のy座標
for (let j = 0; j <= column; j++) {
let tr = Math.PI * 2 / column * j; // ドーナツの各頂点までの角度(ラジアン)
let tx = (rr * irad + orad) * Math.cos(tr); // rrは半径1の円の座標だからiradを掛ける
let ty = ry * irad;
let tz = (rr * irad + orad) * Math.sin(tr);
// ・・・txを求めているところで説明します。
まず最初に、外側ループで求めたx座標rrにirad(断面の半径)を掛けていますね。先ほども書きましたがrrは半径1の断面の座標なので、これに実際の断面の半径を掛けてあげる事で、言わば本当の座標になったというワケです。
で、これにorad(ドーナツの半径)を足してあげると、ドーナツの中心からの位置がでますね。
さらにドーナツの各頂点角度のcosを掛けると最終的なx座標が求められます。なぜcosを掛けるのかよく分からないという方は、関数電卓を使って色々な角度のcosを計算してみるといいと思います。必ず-1から1の値になるので、円を描く時にイイ感じになります。
y座標とz座標も同じような感じですね。雑。
あとがき
最初に見た時は「こんなの絶対分からんだろ」って思いましたが。なんとかなるモンですね。人間の脳はよくできています。
しかし、こういうのを説明するのってホント難しいですね。途中からメンドくさくなってしまいました。まぁ自分用のメモという事で許して頂きましょう。今回は以上です。ありがとうございました。
おしゃれ度
★☆☆☆☆

ディスカッション
コメント一覧
まだ、コメントがありません